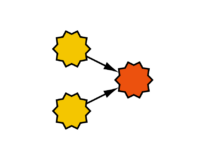Das Perzeptron ist die elementarste Form eines künstlichen neuronalen Netzes. In der einfachsten Variante besteht es aus einem einzigen Neuron mit einem Ausgang und mehreren Eingängen. Mit jedem Eingang ist ein Verbindungsgewicht und mit dem Ausgang eine Aktivierungsfunktion assoziiert. Im einfachsten Fall besteht die Ausgabe aus dem Wert der Aktivierungsfunktion für die gewichtete Summe der Eingaben. Das Lernen eines Perzeptrons erfolgt durch die Anpassung der Gewichtung jeden Neurons unter Verwendung eines Trainingsdatensatzes und der Delta-Regel. Ein Perzeptron mit n Eingängen separiert den Eingaberaum durch eine (n−1)-dimensionale Hyperebene. Dies zeigt die Grenze der Leistungsfähigkeit eines Perzeptrons. Beispielsweise kann die XOR-Funktion nicht durch ein Perzeptron gelernt werden. Das Perzeptron wurde 1958 von Frank Rosenblatt vorgestellt.

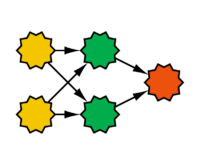Feedforward-Netze sind eine Erweiterung des Perzeptron. Sie besitzen neben der Ausgabeschicht auch eine verdeckte Schicht (hidden layer), diese ist zwischen der Eingabe- und der Ausgabeschicht angesiedelt. Ihre Ausgabe ist außerhalb des Netzes unsichtbar. Charakteristisch für Feedforward-Netze ist, dass zwischen jedem Paar von Knoten von benachbarten Schichten eine Verbindung besteht und dass der Aktivierungsfluss nur von der Eingabe zur Ausgabe erfolgt. Mit Feedforward-Netzen lasst sich die Beschränkung des Perzeptrons überwinden, so kann beispielsweise die XOR-Funktion gelernt werden. Zum Lernen von Feedforward-Netzen wird Backpropagation eingesetzt, es ist eine Verallgemeinerung der Delta-Regel. Dabei wird eine Fehlerfunktion definiert, beispielsweise der quadratische Fehler zwischen gewünschter und tatsächlicher Ausgabe. Für diese Fehlerfunktion wird ein Minimum gesucht, wobei aber häufig lediglich ein lokales Minimum gefunden wird. Dann erfolgt eine Anpassung der Gewichte entgegen des Gradientenanstiegs der Fehlerfunktion.

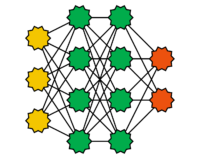Hierbei handelt es sich um Feedforward-Netze mit mehr als einer verdeckten Schicht. Sie werden beim sogenannten Deep Learning verwendet. Mit steigender Anzahl von Schichten und Neuronen steigt auch der Rechenaufwand für das Trainieren von Deep Feedforward-Netzen. Deshalb kommen häufig Rechner mit Manycore Systemen, Grafikprozessoren oder Tensor Processing Units zum Einsatz. Mit Deep Feedforward-Netzen sind in den letzten Jahre spektakuläre Erfolge beispielsweise in der Mustererkennung erzielt worden. Frei verfügbare Softwarebibliotheken für Deep Feedforward-Netze wie beispielsweise TensorFlow oder PyTorch haben in den letzten Jahren für einen breiten Einsatz dieser Netze gesorgt. Beim Trainieren von Deep Feedforward-Netzen werden häufig die Schichten nacheinander betrachtet.

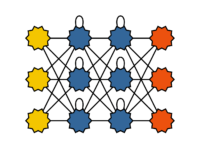Rekurrente neuronale Netze (rückgekoppelte neuronale Netze genannt) haben im Gegensatz zu Feedforward-Netzen auch Verbindungen von Neuronen einer Schicht zu Neuronen derselben oder einer vorangegangenen Schicht. Diese Rekurenz wirkt als Kurzzeitgedächtnis. Rekurrente neuronale Netze eignen sich zum Erlernen von Zeitreihen, beispielsweise zur Klassifikation von temporalen Sequenzen oder zur Zeitreihenvorhersage. Das Training von rekurrenten neuronalen Netzen ist komplexer als das von Feedforward-Netzen. Einer direkten Anwendung von Backpropagation steht die Rückkopplungen entgegen. Rückkopplungen werden häufig durch eine Ausfaltung des Netzes in der Zeit zwischen zwei oder sogar mehreren Eingabedatensätzen bereinigt.

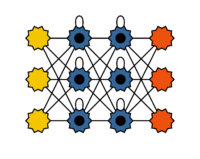
Long Short-Term Memory Netze sind eine besondere Form von rekurrenten neuronalen Netzen. Sie wurden für das Erlernen von Langzeit-Abhängigkeiten entwickelt. Das Kurzzeitgedächtnis von rekurrenten neuronalen Netzen wird dabei zu einem langen Kurzzeitgedächtnis. Das Training mit großen Datenmengen und die Verwendung leistungsfähiger Hardware trugen zum Erfolg der LSTMs bei. Vor allem neuronale Netze mit vielen Schichten profitieren vom Long Short-Term Memory. Das Besondere an Long Short-Term Memory Netzen ist der Aufbau einer Speicherzelle. Sie besteht aus sogenannten Gates. Sie regeln, welche Werte in die Zelle fließen, in der Zelle verbleibt bzw. vergessen werden und die Werte welche weitergegeben werden. LSTMs werden beispielsweise für die Spracherkennung auf Smartphones eingesetzt.

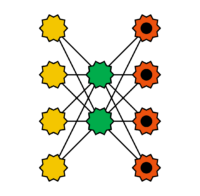Autoencoder sind Feedforward-Netze zum Erlernen von Codierungen. Sie bestehen neben der Eingabeschicht aus mindestens zwei Schichten: Eine Eingabeschicht, einige signifikant kleinere verdeckte Schichten, die die Codierungen bilden und eine Ausgabeschicht, in der jedes Neuron die gleiche Bedeutung hat wie das entsprechende in der Eingabeschicht. Autoencoder erzwingen das Auffinden der besten Repräsentation der Eingabe. Ist die Anzahl der verborgenen Neuronen geringer als die der Eingaben, führt dies zur Dimensionsreduktion. Nach Trainingsende agiert die Eingabeschicht hin zur ersten verborgenen Schicht als Kodierer, analog agiert die letzte verborgene Schicht als Dekodierer. Autoencoder gehören zur Gruppe des unüberwachten Lernens. Spezielle Ausprägungen von Autoencodern sind Stacked Autoencoder und Denoising (stacked) Autoencoder. Bei ersteren werden nach dem Training der ersten beiden Schichten zwei weitere zwischen diese zugefügt und trainiert. Danach können wieder zwischen den neuen Ebenen weitere zwei Ebenen eingefügt und trainiert werden. Denoising Autoencoder werden so trainiert, dass sie aus leicht gestörten Eingaben ungestörte Ausgaben berechnen.

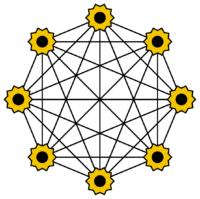Ein Hopfield-Netz ist eine besondere Form eines künstlichen neuronalen Netzes. Es existiert nur eine einzige Schicht, welche gleichzeitig als Ein- und Ausgabeschicht fungiert. Jedes Neuron ist mit jedem, ausgenommen sich selbst, verbunden. Die Neuronen können die Werte −1 und 1 annehmen. Hopfield Netze werden häufig als Assoziativ-Speicher eingesetzt. Sie erlauben die Wiedererkennung von gespeicherten Mustern. In der Trainingsphase werden unvollständige oder verrauschte Muster verwendet. Die Art der Netze wurde 1982 von John Hopfield eingeführt.

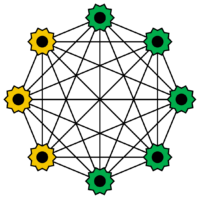Boltzmann-Maschinen sind eine spezielle Art von Hopfield-Netzen. Ein Teil der Neuronen dienen der Eingabe, während der Rest zu einer verdeckten Schicht gehört. Die Neuronen nehmen nur die Werte 0 oder 1 an, sie verhalten sich jedoch stochastisch. Eingabeneuron werden zu Ausgabeneuronen sobald alle verdeckten Neuronen ihren Zustand geändert haben. Das Training von Boltzmann Maschinen erfolgt häufig mit Simulated Annealing. Benannt sind sie nach der Boltzmann Verteilung in der Thermodynamik. Sie wurden 1985 von Geoffrey Hinton und Terrence J. Sejnowski entwickelt.

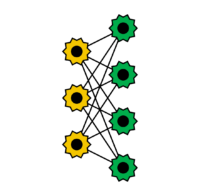Ohne Beschränkung der Verbindungen sind Boltzmann-Maschinen nur sehr schwer trainierbar. Schränkt man die Verbindungen zwischen den Neuronen ein, wird der Lernvorgang stark vereinfacht. Man verzichtet auf Verbindungen zwischen den Eingabe- und den versteckten Neuronen. Restricted Boltzmann Maschine werden in vielen praktischen Anwendungen wie beispielsweise in der Sprachverarbeitung eingesetzt. Das Training erfolgt mittels Backpropagation wie bei Feedforward-Netzen. Restricted Boltzmann Maschines wurden 1986 von Smolensky eingeführt.

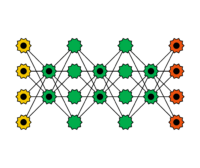Deep Belief Netze sind gekoppelte einfache Netze wie beispielsweise Boltzmann Maschinen oder Autoencoder. Die Idee dabei ist, dass die einzelnen Schichten jeweils ein Feature der Eingabe erkennen und ihre Ausgabe an die nächste Schicht übergeben. Dadurch wird die Eingabe sukzessive gefiltert. Das Training erfolgt in einem Greedy-Stil: Die Schichten werden der Reihe nach einzeln trainiert. Deep Belief Netze finden beispielsweise in Bild- bzw. Videoerkennung eine große Rolle.

Kohonen Netze sind Feedforward-Netze, die neben der Eingabeschicht nur eine weitere Schicht haben, die Kohonen-Schicht. Die Grundidee besteht darin, eine Struktur von zusammenhängenden Verarbeitungseinheiten (Neuronen) zu erstellen. Die Gewichte der Verbindungen werden durch eine unüberwachte Lernregel angepasst. Sie werden zur Klassifikation und zum Clustering eingesetzt. Die Namensgebung geht auf den finnischen Ingenieur Teuvo Kohonen (1982) zurück.

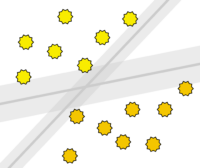Unter Support Vector Maschinen versteht man einen statistischen Ansatz zur Klassifizierung von Objekten in zwei Kategorien. Sie werden sowohl für die lineare als auch für die nicht-lineare Klassifizierung eingesetzt. Die Klassifikation versucht um die Klassengrenzen herum ein möglichst breiten Bereich frei von Objekten zu belassen. Ein Vorteil ist, dass das Verfahren mit verhältnismäßig wenig Trainingsdaten zurechtkommt und dennoch eine hohe Genauigkeit erzielen kann. In der Regel liefert das Verfahren eine schlechtere Performance je verrauschter die Trainingsdaten sind.